what is 0 to the power of 4

Mathematical expression with disputed status

Nada to the power of zero, denoted past 0⁰ , is a mathematical expression with no agreed-upon value. The almost mutual possibilities are 1 or leaving the expression undefined, with justifications existing for each, depending on context. In algebra and combinatorics, the generally agreed upon value is0⁰ = 1, whereas in mathematical analysis, the expression is sometimes left undefined. Estimator programming languages and software too have differing ways of treatment this expression.

Detached exponents [edit]

Many widely used formulas involving natural-number exponents require 0⁰ to be divers as ane. For example, the following three interpretations of b ⁰ make only every bit much sense for b = 0 as they do for positive integers b:

• The estimation of b ⁰ as an empty product assigns information technology the value 1.
• The combinatorial interpretation of b ⁰ is the number of 0-tuples of elements from a b -chemical element gear up; there is exactly one 0-tuple.
• The set-theoretic estimation of b ⁰ is the number of functions from the empty set to a b -element set; there is exactly one such function, namely, the empty function.^[1]

All three of these specialize to give 0⁰ = 1.

Polynomials and power series [edit]

When working with polynomials, it is user-friendly to define 0⁰ equally 1. A (existent) polynomial is an expression of the class a ₀ x ⁰ + ⋅⋅⋅ + a _{due north} x ⁿ , where 10 is an indeterminate, and the coefficients a _n are existent numbers. Polynomials are added termwise, and multiplied by applying the distributive police force and the usual rules for exponents. With these algebraic rules for manipulation, polynomials grade a ring R[ten]. The polynomial ten ⁰ is the multiplicative identity of the polynomial ring, pregnant that it is the element such that x ⁰ times any polynomial p(x) is simply p(ten).^[2] Polynomials can be evaluated by specializing x to a existent number. More precisely, for whatever given real number r , there is a unique unital R -algebra homomorphism ev _r  : R[ten] → R such that ev _r (x) = r . Because ev _r is unital, ev _r (x ⁰) = 1. That is, r ⁰ = 1 for each real number r , including 0. The aforementioned statement applies with R replaced by whatever ring.^[3]

Defining 0⁰ = one is necessary for many polynomial identities. For example, the binomial theorem (i + x) ⁿ = ∑ ⁿ
_k=0 ( ^north
_k ) x ^k is not valid for x = 0 unless 0⁰ = ane.^[4]

Similarly, rings of power series crave x ⁰ to be defined as 1 for all specializations of x . For instance, identities similar 1 / 1−x = ∑ ^∞
_north=0 ten ⁿ and east ¹⁰ = ∑ ^∞
_n=0 x ^north / n! agree for 10 = 0 only if 0⁰ = 1.^[five]

In order for the polynomial x ⁰ to define a continuous function R → R , ane must ascertain 0⁰ = 1.

In calculus, the power dominion d / dx 10 ^{due north} = nx ⁿ⁻¹ is valid for due north = 1 at x = 0 only if 0⁰ = 1.

Continuous exponents [edit]

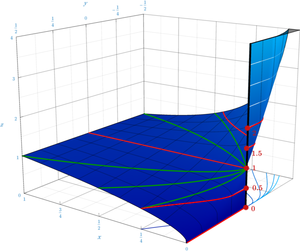
Plot of z = ten ^y . The red curves (with z abiding) yield different limits as (x, y) approaches (0, 0). The dark-green curves (of finite constant slope, y = ax ) all yield a limit of ane.

Limits involving algebraic operations tin can frequently exist evaluated by replacing subexpressions past their limits; if the resulting expression does non determine the original limit, the expression is known as an indeterminate grade.^[half-dozen] The expression 0⁰ is an indeterminate course: Given existent-valued functions f(t) and g(t) budgeted 0 (as t approaches a real number or ±∞) with f(t) > 0, the limit of f(t) ^g(t) can be any non-negative real number or +∞, or it can diverge, depending on f and m. For example, each limit beneath involves a function f(t) ^g(t) with f(t), yard(t) → 0 equally t → 0⁺ (a one-sided limit), but their values are different:

$${\displaystyle \lim _{t\to 0^{+}}{t}^{t}=1,}$$

$${\displaystyle \lim _{t\to 0^{+}}\left(eastward^{-ane/t^{2}}\correct)^{t}=0,}$$

$${\displaystyle \lim _{t\to 0^{+}}\left(e^{-1/t^{two}}\right)^{-t}=+\infty ,}$$

$${\displaystyle \lim _{t\to 0^{+}}\left(e^{-1/t}\right)^{at}=e^{-a}.}$$

Thus, the two-variable function x ^y , though continuous on the fix {(ten, y) : x > 0}, cannot exist extended to a continuous function on {(ten, y) : x > 0} ∪ {(0, 0)}, no thing how 1 chooses to define 0⁰ .^[7]

On the other hand, if f and yard are both analytic functions on an open neighborhood of a number c, then f(t) ^g(t) → ane every bit t approaches c from whatsoever side on which f is positive.^[8]

Rotando and Korn^[9] showed that if ${\displaystyle f}$ and ${\displaystyle g}$ are real functions that vanish at the origin and are analytic at 0, then ${\displaystyle \lim _{x\to 0^{+}}f(x)^{m(ten)}=1}$ . The same conclusion was deduced past Baxley and Hayashi,^[10] who also obtained a more general upshot in which no smoothness conditions are required. More general sufficient weather for ${\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}m(10)=0}$ implying ${\displaystyle \lim _{ten\to c}f(x)^{g(10)}=1}$ have been found.^[11]

Circuitous exponents [edit]

In the complex domain, the role z ^w may be defined for nonzero z past choosing a co-operative of log z and defining z ^w every bit east ^{w log z} . This does not define 0 ^{due west} since there is no co-operative of log z defined at z = 0, let solitary in a neighborhood of 0.^{[12] [13] [xiv]}

History [edit]

Equally a value [edit]

In 1752, Euler in Introductio in analysin infinitorum wrote that a ⁰ = ane ^[xv] and explicitly mentioned that 0⁰ = ane.^[16] An note attributed^[17] to Mascheroni in a 1787 edition of Euler'due south book Institutiones calculi differentialis ^[eighteen] offered the "justification"

$${\displaystyle 0^{0}=(a-a)^{northward-n}={\frac {(a-a)^{n}}{(a-a)^{due north}}}=1}$$

every bit well equally some other more involved justification. In the 1830s, Libri^{[19] [17]} published several further arguments attempting to justify the merits 0⁰ = i, though these were far from convincing, even by standards of rigor at the time.^[twenty]

As a limiting grade [edit]

Euler, when setting 0⁰ = 1, mentioned that consequently the values of the function 0 ^x take a "huge jump", from ∞ for x < 0, to 1 at 10 = 0, to 0 for x > 0.^[15] In 1814, Pfaff used a squeeze theorem argument to prove that x ¹⁰ → 1 as x → 0⁺ .^[8]

On the other hand, in 1821 Cauchy^[21] explained why the limit of ten ^y every bit positive numbers ten and y approach 0 while being constrained by some stock-still relation could be made to presume any value between 0 and ∞ past choosing the relation appropriately. He deduced that the limit of the full ii-variable office x ^y without a specified constraint is "indeterminate". With this justification, he listed 0⁰ along with expressions like 0 / 0 in a table of indeterminate forms.

Plainly unaware of Cauchy's piece of work, Möbius^[8] in 1834, building on Pfaff's argument, claimed incorrectly that f(x) ^chiliad(x) → 1 whenever f(ten),g(x) → 0 as ten approaches a number c (presumably f is assumed positive away from c). Möbius reduced to the case c = 0, simply so made the mistake of assuming that each of f and g could be expressed in the grade Px ⁿ for some continuous part P not vanishing at 0 and some nonnegative integer northward, which is truthful for analytic functions, simply not in full general. An anonymous commentator pointed out the unjustified step;^[22] so another commentator who signed his name only every bit "South" provided the explicit counterexamples (east ^−1/x ) ^x → eastward ^−one and (east ^−1/ten )^twox → e ⁻² as ten → 0⁺ and expressed the situation by writing that "0⁰ tin have many different values".^[22]

Electric current situation [edit]

• Some authors define 0⁰ equally 1 because it simplifies many theorem statements. According to Benson (1999), "The choice whether to define 0⁰ is based on convenience, not on definiteness. If we refrain from defining 0⁰ , then certain assertions become unnecessarily awkward. ... The consensus is to use the definition 0⁰ = 1, although there are textbooks that refrain from defining 0⁰ ."^[23] Knuth (1992) contends more strongly that 0⁰ "has to be 1"; he draws a distinction betwixt the value 0⁰ , which should equal one, and the limiting class 0⁰ (an abridgement for a limit of f(t) ^g(t) where f(t), thou(t) → 0), which is an indeterminate form: "Both Cauchy and Libri were correct, only Libri and his defenders did not understand why truth was on their side."^[20]
• Other authors get out 0⁰ undefined because 0⁰ is an indeterminate form: f(t), g(t) → 0 does non imply f(t) ^g(t) → ane.^{[24] [25]}

There do not seem to be any authors assigning 0⁰ a specific value other than i.^[23]

Treatment on computers [edit]

IEEE floating-point standard [edit]

The IEEE 754-2008 floating-point standard is used in the design of nigh floating-point libraries. Information technology recommends a number of operations for computing a power:^[26]

• pown (whose exponent is an integer) treats 0⁰ as 1; see § Discrete exponents.
• pow (whose intent is to return a not-NaN issue when the exponent is an integer, like pown) treats 0⁰ as i.
• powr treats 0⁰ as NaN (Not-a-Number) due to the indeterminate class; see § Continuous exponents.

The prisoner of war variant is inspired by the pw part from C99, mainly for compatibility.^[27] It is useful mostly for languages with a single power role. The pown and powr variants accept been introduced due to conflicting usage of the power functions and the dissimilar points of view (as stated to a higher place).^[28]

Programming languages [edit]

The C and C++ standards practice not specify the event of 0⁰ (a domain error may occur). Merely for C, as of C99, if the normative annex F is supported, the result for real floating-betoken types is required to exist 1 because there are meaning applications for which this value is more useful than NaN ^[29] (for instance, with detached exponents); the result on complex types is not specified, even if the informative addendum G is supported. The Coffee standard,^[thirty] the .Net Framework method System.Math.Pow,^[31] Julia, and Python^{[32] [33]} too treat 0⁰ as one. Some languages document that their exponentiation operation corresponds to the prisoner of war function from the C mathematical library; this is the instance with Lua^[34] and Perl's ** operator^[35] (where it is explicitly mentioned that the upshot of 0**0 is platform-dependent).

Mathematical and scientific software [edit]

APL,^{[ commendation needed ]} R,^[36] Stata, SageMath,^[37] Matlab, Magma, GAP, Singular, PARI/GP,^[38] and GNU Octave evaluate x ⁰ to 1. Mathematica^[39] and Macsyma simplify ten ⁰ to 1 even if no constraints are placed on x ; however, if 0⁰ is entered directly, it is treated as an error or indeterminate. SageMath does not simplify 0 ^x . Maple, Mathematica^[39] and PARI/GP^{[38] [40]} further distinguish betwixt integer and floating-point values: If the exponent is a zero of integer type, they render a 1 of the blazon of the base; exponentiation with a floating-point exponent of value zero is treated equally undefined, indeterminate or error.

References [edit]

1. ^ Bourbaki, Nicolas (2004). "III.§three.5". Elements of Mathematics, Theory of Sets. Springer-Verlag.
2. ^ Bourbaki, Nicolas (1970). "§III.2 No. nine". Algèbre. Springer. 50'unique monôme de degré 0 est l'élément unité de A[(10 _i ) _i∈I ]; on l'identifie souvent à l'élément unité one de A
3. ^ Bourbaki, Nicolas (1970). "§Iv.ane No. three". Algèbre. Springer.
4. ^ Graham, Ronald; Knuth, Donald; Patashnik, Oren (1989-01-05). "Binomial coefficients". Concrete Mathematics (1st ed.). Addison-Wesley Longman Publishing Co. p. 162. ISBN0-201-14236-8. Some textbooks leave the quantity 0⁰ undefined, because the functions x ⁰ and 0 ¹⁰ have different limiting values when x decreases to 0. But this is a error. We must define x ⁰ = ane, for all ten , if the binomial theorem is to exist valid when x = 0, y = 0, and/or x = −y . The binomial theorem is too important to be arbitrarily restricted! Past contrast, the office 0 ^x is quite unimportant.
5. ^ Vaughn, Herbert E. (1970). "The expression 0⁰ ". The Mathematics Instructor. 63: 111–112.
6. ^ Malik, S. C.; Arora, Savita (1992). Mathematical Assay. New York, The states: Wiley. p. 223. ISBN978-81-224-0323-7. In full general the limit of φ(10)/ψ(x) when x = a in example the limits of both the functions exist is equal to the limit of the numerator divided by the denominator. But what happens when both limits are zero? The sectionalisation (0/0) and so becomes meaningless. A example like this is known as an indeterminate form. Other such forms are ∞/∞, 0 × ∞, ∞ − ∞, 0⁰ , i^∞ and ∞⁰ .
7. ^ Paige, 50. J. (March 1954). "A note on indeterminate forms". American Mathematical Monthly. 61 (iii): 189–190. doi:10.2307/2307224. JSTOR 2307224.
8. ^ ^{a b c} Möbius, A. F. (1834). "Beweis der Gleichung 0⁰ = i, nach J. F. Pfaff" [Proof of the equation 0⁰ = 1, co-ordinate to J. F. Pfaff]. Journal für die reine und angewandte Mathematik (in German). 1834 (12): 134–136. doi:10.1515/crll.1834.12.134. S2CID 199547186.
9. ^ Rotando, Louis Yard.; Korn, Henry (1977). "The Indeterminate Grade 0^0". Mathematics Mag. 50 (1): 41–42. doi:10.1080/0025570X.1977.11976612. Retrieved 2021-11-23 .
10. ^ Baxley, John V.; Hayashi, Elmer M. (June 1978). "Indeterminate Forms of Exponential Blazon". The American Mathematical Monthly. 85 (6): 484–486. doi:10.2307/2320074. JSTOR 2320074. Retrieved 2021-11-23 .
11. ^ Xiao, Jinsen; He, Jianxun (Dec 2017). "On Indeterminate Forms of Exponential Blazon". Mathematics Mag. 90 (5): 371–374. doi:10.4169/math.mag.90.v.371. JSTOR 10.4169/math.mag.90.v.371. S2CID 125602000. Retrieved 2021-eleven-23 .
12. ^ Carrier, George F.; Krook, Max; Pearson, Carl E. (2005). Functions of a Complex Variable: Theory and Technique. p. 15. ISBN0-89871-595-four. Since log(0) does not exist, 0 ^z is undefined. For Re(z) > 0, we define information technology arbitrarily as 0.
13. ^ Gonzalez, Mario (1991). Classical Complex Analysis. Chapman & Hall. p. 56. ISBN0-8247-8415-4. For z = 0, w ≠ 0, we ascertain 0 ^w = 0, while 0⁰ is non divers.
14. ^ Meyerson, Mark D. (June 1996). "The x ^ten Spindle". Mathematics Magazine. Vol. 69, no. 3. pp. 198–206. doi:10.1080/0025570X.1996.11996428. ... Let'due south start at x = 0. Hither x ^ten is undefined.
15. ^ ^{a b} Euler, Leonhard (1988). "Chapter six, §97". Introduction to analysis of the space, Book 1. Translated by Blanton, J. D. Springer. p. 75. ISBN978-0-387-96824-7.
16. ^ Euler, Leonhard (1988). "Chapter 6, §99". Introduction to analysis of the infinite, Book 1. Translated past Blanton, J. D. Springer. p. 76. ISBN978-0-387-96824-7.
17. ^ ^{a b} Libri, Guillaume (1833). "Mémoire sur les fonctions discontinues". Journal für die reine und angewandte Mathematik (in French). 1833 (10): 303–316. doi:10.1515/crll.1833.ten.303. S2CID 121610886.
18. ^ Euler, Leonhard (1787). Institutiones calculi differentialis, Vol. ii. Ticini. ISBN978-0-387-96824-7.
19. ^ Libri, Guillaume (1830). "Note sur les valeurs de la fonction 0^{0 ten} ". Periodical für die reine und angewandte Mathematik (in French). 1830 (6): 67–72. doi:10.1515/crll.1830.half dozen.67. S2CID 121706970.
20. ^ ^{a b} Knuth, Donald E. (1992). "Two Notes on Notation". The American Mathematical Monthly. 99 (5): 403–422. arXiv:math/9205211. Bibcode:1992math......5211K. doi:ten.1080/00029890.1992.11995869.
21. ^ Cauchy, Augustin-Louis (1821), Cours d'Analyse de fifty'École Royale Polytechnique, Oeuvres Complètes: two (in French), vol. 3, pp. 65–69
22. ^ ^{a b} Anonymous (1834). "Bemerkungen zu dem Aufsatze überschrieben "Beweis der Gleichung 0⁰ = 1, nach J. F. Pfaff"" [Remarks on the essay "Proof of the equation 0⁰ = 1, according to J. F. Pfaff"]. Periodical für dice reine und angewandte Mathematik (in German language). 1834 (12): 292–294. doi:ten.1515/crll.1834.12.292.
23. ^ ^{a b} Benson, Donald C. (1999). Written at New York, USA. The Moment of Proof: Mathematical Epiphanies. Oxford, Uk: Oxford University Press. p. 29. ISBN978-0-19-511721-nine.
24. ^ Edwards; Penney (1994). Calculus (quaternary ed.). Prentice-Hall. p. 466.
25. ^ Keedy; Bittinger; Smith (1982). Algebra Two. Addison-Wesley. p. 32.
26. ^ Muller, Jean-Michel; Brisebarre, Nicolas; de Dinechin, Florent; Jeannerod, Claude-Pierre; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Stehlé, Damien; Torres, Serge (2010). Handbook of Floating-Point Arithmetic (1 ed.). Birkhäuser. p. 216. doi:10.1007/978-0-8176-4705-6. ISBN978-0-8176-4704-nine. LCCN 2009939668. ISBN 978-0-8176-4705-6 (online), ISBN 0-8176-4704-X (impress)
27. ^ "More transcendental questions". grouper.ieee.org. Archived from the original on 2017-xi-14. Retrieved 2019-05-27 . (NB. Beginning of the discussion about the power functions for the revision of the IEEE 754 standard, May 2007.)
28. ^ "Re: A vague specification". grouper.ieee.org. Archived from the original on 2017-11-14. Retrieved 2019-05-27 . (NB. Suggestion of variants in the discussion nearly the power functions for the revision of the IEEE 754 standard, May 2007.)
29. ^ Rationale for International Standard—Programming Languages—C (PDF) (Study). Revision 5.10. April 2003. p. 182.
30. ^ "Math (Java Platform SE 8) pow". Oracle.
31. ^ ".NET Framework Class Library Math.Pw Method". Microsoft.
32. ^ "Congenital-in Types — Python 3.8.1 documentation". Retrieved 2020-01-25 . Python defines pow(0, 0) and 0 ** 0 to be 1, equally is common for programming languages.
33. ^ "math — Mathematical functions — Python 3.8.1 documentation". Retrieved 2020-01-25 . Exceptional cases follow Annex 'F' of the C99 standard every bit far as possible. In particular, pow(ane.0, x) and pow(ten, 0.0) e'er return 1.0, fifty-fifty when ten is a aught or a NaN.
34. ^ "Lua 5.3 Reference Manual". Retrieved 2019-05-27 .
35. ^ "perlop – Exponentiation". Retrieved 2019-05-27 .
36. ^ The R Core Team (2019-07-05). "R: A Language and Environs for Statistical Calculating – Reference Index" (PDF). Version iii.6.1. p. 23. Retrieved 2019-eleven-22 . i ^ y and y ^ 0 are 1, ever.
37. ^ The Sage Evolution Squad (2020). "Sage 9.ii Reference Manual: Standard Commutative Rings. Elements of the ring Z of integers". Retrieved 2021-01-21 . For consistency with Python and MPFR, 0^0 is defined to be 1 in Sage.
38. ^ ^{a b} "pari.git / commitdiff – ten- x ^ t_FRAC: return an exact result if possible; e.g. 4^(i/2) is at present ii". Retrieved 2018-09-10 .
39. ^ ^{a b} "Wolfram Language & Organization Documentation: Power". Wolfram. Retrieved 2018-08-02 .
40. ^ The PARI Grouping (2018). "Users' Guide to PARI/GP (version 2.xi.0)" (PDF). pp. 10, 122. Retrieved 2018-09-04 . In that location is too the exponentiation operator ^, when the exponent is of blazon integer; otherwise, information technology is considered every bit a transcendental function. ... If the exponent n is an integer, and so verbal operations are performed using binary (left-shift) powering techniques. ... If the exponent n is not an integer, powering is treated as the transcendental function exp(due north log x).

External links [edit]

• sci.math FAQ: What is 0⁰ ?
• What does 0⁰ (zero to the zeroth power) equal? on AskAMathematician.com

cramptwelord.blogspot.com

Source: https://en.wikipedia.org/wiki/Zero_to_the_power_of_zero

Share :